Glavne vrste neenakosti in njihove lastnosti. Reševanje eksponentnih neenačb: osnovne metode
Kako rešiti linearne neenačbe? Za začetek moramo neenakost poenostaviti: odprite oklepaje in prinesite podobne izraze.
Oglejmo si primere reševanja linearnih neenačb z eno spremenljivko.
Odpiranje oklepaja. Če je pred oklepajem faktor, ga pomnožite z vsakim členom v oklepaju. Če je pred oklepajem znak plus, se znaki v oklepaju ne spremenijo. Če je pred oklepajem znak minus, sta znaka v oklepaju obrnjena.
Predstavljamo podobne pogoje.
Dobili smo neenačbo oblike ax+b≤cx+d. Neznanke premaknemo na eno stran, znane na drugo z nasprotnimi predznaki (lahko bi najprej premaknili neznanke na eno stran, znane na drugo in šele nato prinesli podobne člene).
Obe strani neenakosti delimo s številom pred X. Ker je 8 večje od nič, se znak neenakosti ne spremeni:
Title="Upodobilo QuickLaTeX.com">!}
Ker , je točka -2 označena na številski premici kot osenčena. od -2 do minus neskončnosti. ![]()
Ker neenakost ni stroga in je pika zasenčena, zapišemo odgovor -2 z oglatim oklepajem.
![]()
Če želite preiti z decimalnih mest na cela števila, lahko obe strani neenakosti pomnožite z 10 (to ni potrebno. Delate lahko z decimalnimi števili).
Title="Upodobilo QuickLaTeX.com">!}
Ko obe strani pomnožimo s pozitivnim številom, se znak neenakosti ne spremeni. Vsak izraz je treba pomnožiti z 10. Pri množenju zmnožka z 10 uporabimo asociativno lastnost množenja, torej z 10 pomnožimo samo en faktor.
Razširitev oklepajev:
Tukaj so podobni izrazi:
Neznanke premikamo v eno smer, znane v drugo z nasprotnimi predznaki:
Obe strani neenakosti delimo s številom pred X. Ker je -6 negativno število, je znak neenakosti obrnjen:
Title="Upodobilo QuickLaTeX.com">!}
Zmanjšamo ulomek:
Title="Upodobilo QuickLaTeX.com">!}
Ker je neenakost stroga, označimo -2/3 na številski premici s preluknjano piko. Senčenje gre v desno, do plus neskončnosti: ![]()
Neenakost je stroga, manjka pika, zato odgovor -2/3 zapišemo z oklepajem:
![]()
Title="Upodobilo QuickLaTeX.com">!}
Odpiranje oklepaja. Če je pred zmnožkom dveh oklepajev znak minus, je priročno najprej izvesti množenje in šele nato odpreti oklepaje, tako da spremenite znak vsakega izraza v nasprotno:
Title="Upodobilo QuickLaTeX.com">!}
Title="Upodobilo QuickLaTeX.com">!}
Title="Upodobilo QuickLaTeX.com">!}
Title="Upodobilo QuickLaTeX.com">!}
Tukaj so podobni izrazi:
Title="Upodobilo QuickLaTeX.com">!}
Neznane - v eno smer, znane - v drugo z nasprotnimi predznaki:
Title="Upodobilo QuickLaTeX.com">!}
Title="Upodobilo QuickLaTeX.com">!}
Obe strani neenakosti delimo s številom pred X. Od -10<0, знак неравенства меняется на противоположный:
Ker je neenakost stroga, označimo 1,6 na številski premici s preluknjano piko. Senčenje od 1,6 gre v levo do minus neskončnosti: ![]()
Ker je neenakost stroga in manjka pika, zapišemo 1,6 pri odgovoru z oklepajem.
Koncept matematične neenakosti se je pojavil v starih časih. To se je zgodilo, ko je pračlovek začel primerjati njihovo količino in velikost pri štetju in rokovanju z različnimi predmeti. Arhimed, Evklid in drugi znani znanstveniki: matematiki, astronomi, oblikovalci in filozofi so že od antičnih časov uporabljali neenakosti pri svojem razmišljanju.
Toda v svojih delih so praviloma uporabljali besedno terminologijo. V Angliji so prvič izumili in uveljavili sodobne znake za označevanje pojmov "več" in "manj" v obliki, v kateri jih danes pozna vsak šolar. Matematik Thomas Harriot je svojim potomcem zagotovil takšno storitev. In to se je zgodilo pred približno štirimi stoletji.
Znanih je veliko vrst neenakosti. Med njimi so preprosta, ki vsebujejo eno, dve ali več spremenljivk, kvadratna, frakcijska, kompleksna razmerja in celo tista, ki jih predstavlja sistem izrazov. Najboljši način za razumevanje reševanja neenakosti je uporaba različnih primerov.
Ne zamudite vlaka
Za začetek si predstavljajmo, da prebivalec podeželja hiti na železniško postajo, ki se nahaja 20 km od njegove vasi. Da ne bi zamudil vlaka, ki odhaja ob 11. uri, mora pravočasno zapustiti hišo. Ob kateri uri naj to stori, če je njegova hitrost 5 km/h? Rešitev tega praktičnega problema se zmanjša na izpolnitev pogojev izraza: 5 (11 - X) ≥ 20, kjer je X čas odhoda.
To je razumljivo, saj je razdalja, ki jo mora vaščan premagati do postaje, enaka hitrosti gibanja, pomnoženi s številom ur na poti. Človek lahko pride zgodaj, ne more pa zamujati. Če boste znali rešiti neenakosti in svoje veščine uporabili v praksi, boste na koncu dobili X ≤ 7, kar je odgovor. To pomeni, da naj gre vaščan na železniško postajo ob sedmih zjutraj ali malo prej.
Številski intervali na koordinatni premici
Zdaj pa poglejmo, kako preslikati opisane relacije na Zgoraj dobljena neenakost ni stroga. To pomeni, da lahko spremenljivka sprejme vrednosti, manjše od 7, ali pa je enaka temu številu. Navedimo druge primere. Če želite to narediti, skrbno preglejte štiri spodnje slike.

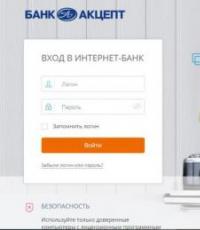
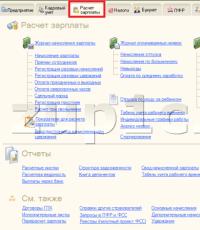
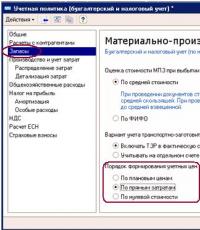
Na prvem od njih lahko vidite grafični prikaz intervala [-7; 7]. Sestavljen je iz niza števil, postavljenih na koordinatno črto in med -7 in 7, vključno z mejami. V tem primeru so točke na grafu upodobljene kot zapolnjeni krogi, interval pa je zabeležen z uporabo
Druga slika je grafični prikaz stroge neenakosti. V tem primeru mejni števili -7 in 7, prikazani s preluknjanimi (nezapolnjenimi) pikami, nista vključeni v navedeni niz. In sam interval je zapisan v oklepajih na naslednji način: (-7; 7).
To pomeni, da ko smo ugotovili, kako rešiti neenakosti te vrste in prejeli podoben odgovor, lahko sklepamo, da je sestavljena iz števil, ki so med zadevnimi mejami, razen -7 in 7. Naslednja dva primera je treba ovrednotiti v podoben način. Tretja slika prikazuje slike intervalov (-∞; -7] U . -
Diapozitiv 19
Grafično rešite neenačbe:
1).x²-3x 0; 3).x²+2x≥0; 4). -2x²+x+1≤0; (0;3) (-∞;0)U(4;+∞) (-∞;-2]UU)